schedule2019-02-19

P5jsでガウス分布のデータセットを作成する

simulationアルゴリズムJavaScriptp5js

k-meansのクラスタリングを可視化するために、偏りのあるデータセットを作成します。 P5jsの関数randomGaussian()を使って２次元の混合分布を表現しました。

今回作成したp5jsのGIF

gif

P5jsのランダム関数

P5jsには分布が異なるランダム関数が２種類あります。

random()は一様分布の乱数、randomGaussian()はガウス分布（正規分布）をとる乱数を返します。

ガウス分布

ガウス分布は平均値の付近に集積するような釣鐘型の確率分布です。正規分布とも呼びます。

平均を $\mu$ , 分散を $\sigma^2 > 0$ とする（1次元）正規分布とは、確率密度関数が次の形です。

f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{-\frac{(x-\mu)^2}{2\sigma^2}}

この分布は $N(\mu, \sigma^2)$ と表します。

wikiより引用

randomGaussian()

P5jsの関数randomGaussian()は、ガウス分布に従った乱数を返します。使い方は以下の通りです。

引数を渡さずデフォルトでは $N(0, 1)$ の標準正規分布を返します。

let x = randomGaussian();

平均10、標準偏差10のガウス分布 $N(10, 10)$ を返すには以下のようにします。

let mean = 10; // 平均
let stddiv = 10; // 標準偏差

let x = randomGaussian(mean, stddiv);

標準偏差は英語でstandard deviationです。

平均値から極端に離れた値が帰る確率はかなり低いですが、理論的に返り値に最大最小値はありません。

２次元平面にクラスターをプロットする

k-meansの可視化に利用するため、randomGaussian()を使って２次元平面に偏りのあるクラスターのデータセットをプロットします。

各クラスターは、x, y軸それぞれにガウス分布を持つ多変量正規分布のクラスタにしています。

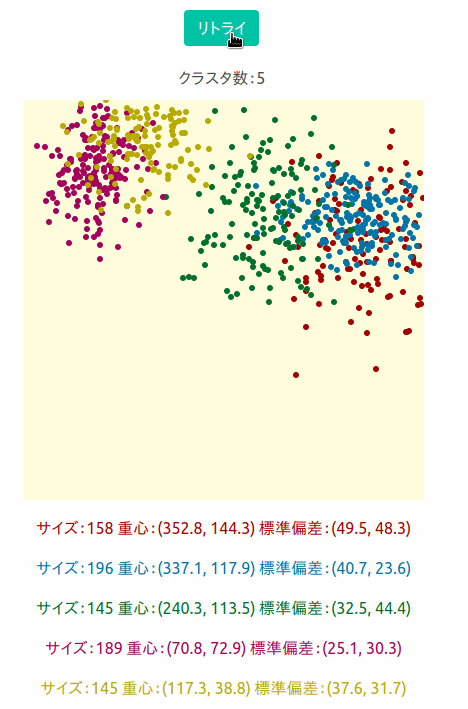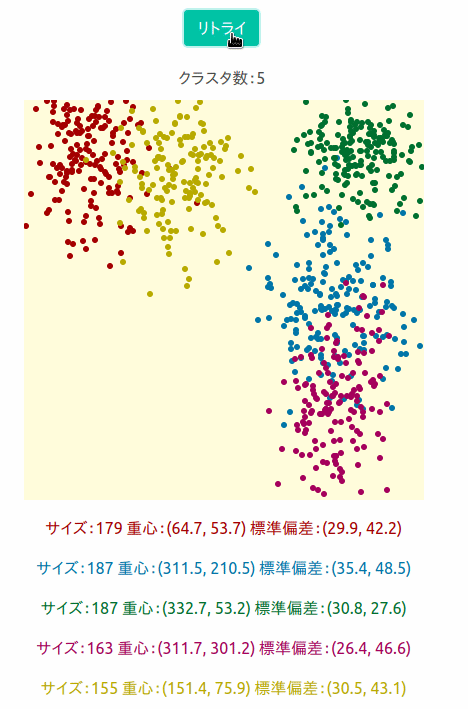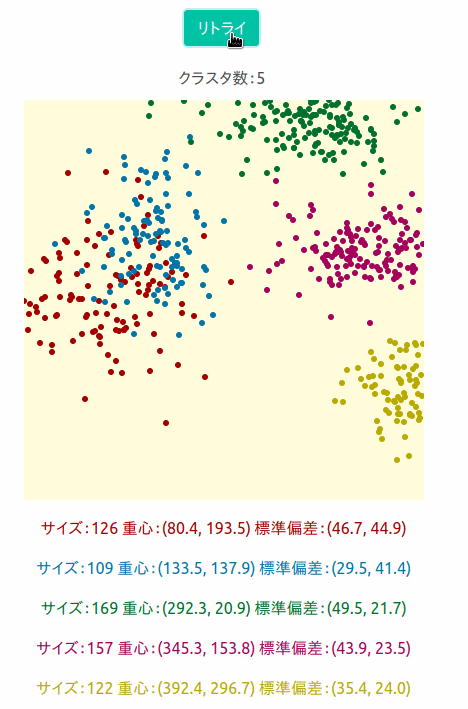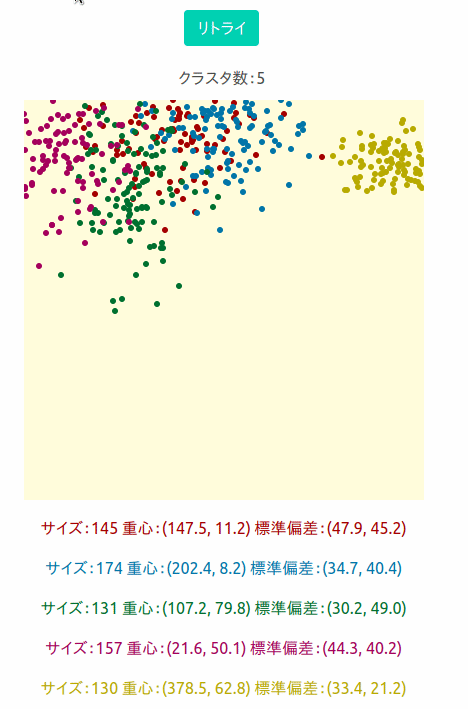
出来たものが下の画像です。400×400のキャンバスに５つのクラスターがランダムに現れるようにしました。

程よくバラけたもの。

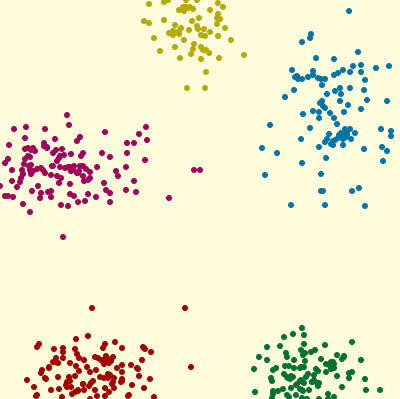
cluster1

重なりがあるクラスター。

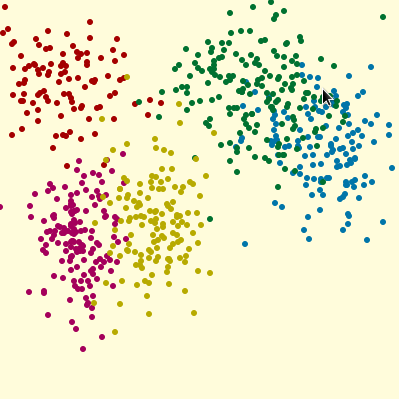
cluster2

k-meansのクラスタ数を5とすると、上の程よくバラけた点群は正確に分類出来そうです。下の点群は、クラスタ数３がちょうど良さそうな感じですね。

シミュレーション

実際にシミュレーションしているのが下の図です。

ひとつのクラスターに約150個のデータができるようにしています。 リトライを押すと新しいデータセットを作成します。

それぞれのクラスターのサイズと重心位置(x_mean, y_mean)、標準偏差（x_stddiv, y_stddiv）を表示ししています。

ソースコードと解説

データセットの作成

コードの中でデータセットを作成する部分の解説。

描画するキャンバスのサイズが400×400(px)としているので、その中で程よくバラけるようにパラメータを調節しています。配列の要素に[x, y]となる座標を追加している。また、キャンバスの範囲外は削除するようにしています。

let canvas_size = { width: 400, height: 400 } //px

// ランダムな混合分布のデータセットを作成
function createData() {
  let clusters = [];
  for (let i = 0; i < 5; i++) {
    let size = int(random(100, 200));
    let x_mean = random(0, canvas_size.width);
    let y_mean = random(0, canvas_size.height);
    let x_stddiv = random(20, 50);
    let y_stddiv = random(20, 50);

    let c = createGaussianDistribution(size, x_mean, x_stddiv, y_mean, y_stddiv);
    clusters.push(c);
  }

  return clusters;
}

// ガウシアン分布から乱数で生成する
function createGaussianDistribution(size, x_mean, x_stddiv, y_mean, y_stddiv) {
  // 点群のリスト
  let array = [];
  for (let i = 0; i < size; i++) {
    // ガウシアン分布のランダムな値
    let x = randomGaussian(x_mean, x_stddiv);
    let y = randomGaussian(y_mean, y_stddiv);
    // 範囲外のポイントは除く
    if (isOut(x, y)) continue;
    array.push([x, y]);
  }
  return array;
}

ソースコード全文

キャンバスと表示制御部分のhtml

<!-- p5js -->
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.7.3/p5.min.js"></script>
<script src="/images/posts/98/gaussian-distribution.js"></script>

<div class="p5js">
  <div class="center">
    <button type="button" class="button is-primary" onclick="retry();">リトライ</button>&nbsp;
  </div>
  <div  class="center">
    クラスタ数：<span id="count">5</span>&nbsp;
  </div>
  <div id="canvas"  class="has-text-centered"></div>
  <div class="center" id="parameters"></div>
</div>

<style>
.p5js .center{
  text-align: center;
  margin: 10px;
}
.p5js .button{
  text-align: center;
  margin: 10px;
}
</style>

gaussian-distribution.js

let data = [];
let frame_rate = 10;
let parameter = [];

let canvas_size = { width: 400, height: 400 } //px

let bg_color = '#FFFCDB';
let cluster_colors = ['#A40000', '#0075A9', '#007130', '#A4005B', '#B7AA00', '#100964'];

// 再描画
function retry() {
  ini();
}

// 初期化
function ini() {
  parameter = [];
  data = createData();
  displayParameters();
}

// パラメータの表示
function displayParameters(){
  let html = '';
  for(let i in parameter){
    let p = parameter[i];
    let txt = '<p style="color:' + cluster_colors[i]+ ';">';
    txt += 'サイズ：' + p.size +'&nbsp;';
    txt += '重心：(' + p.mean.x.toFixed(1) + ', ' + p.mean.y.toFixed(1)+')&nbsp;';
    txt += '標準偏差：(' + p.stddiv.x.toFixed(1) + ', ' + p.stddiv.y.toFixed(1) +')</p>';
    html += txt;
  }
  document.getElementById('parameters').innerHTML = html;
}

// ランダムな混合分布のデータセットを作成
function createData() {
  let clusters = [];
  for (let i = 0; i < 5; i++) {
    let size = int(random(100, 200));
    let x_mean = random(0, canvas_size.width);
    let y_mean = random(0, canvas_size.height);
    let x_stddiv = random(20, 50);
    let y_stddiv = random(20, 50);

    let c = createGaussianDistribution(size, x_mean, x_stddiv, y_mean, y_stddiv);
    clusters.push(c);
  }

  return clusters;
}

// ガウシアン分布から乱数で生成する
function createGaussianDistribution(size, x_mean, x_stddiv, y_mean, y_stddiv) {
  // パラメータ表示用
  parameter.push({ 
    size: size,
    mean: { x: x_mean, y: y_mean },
    stddiv: { x: x_stddiv, y: y_stddiv }
  });
  // 点群のリスト
  let array = [];
  for (let i = 0; i < size; i++) {
    // ガウシアン分布のランダムな値
    let x = randomGaussian(x_mean, x_stddiv);
    let y = randomGaussian(y_mean, y_stddiv);
    // 範囲外のポイントは除く
    if (isOut(x, y)) continue;
    array.push([x, y]);
  }
  return array;
}

// 描画範囲外か判定
function isOut(x, y) {
  if (x < 0 || canvas_size.width < x ||
    y < 0 || canvas_size.height < y) {
    return true;
  }
  return false;
}


// p5js
function setup() {
  let canvas = createCanvas(canvas_size.width, canvas_size.height);
  canvas.parent('canvas');
  // フーレームレートを1/1secにする
  frameRate(frame_rate);

  background(color(bg_color));

  // 描画を繰り返さない。
  ini();
}

function draw() {
  // 描画
  background(color(bg_color));
  drawCluster();
}

// 混合分布の描画
function drawCluster() {
  for (let i in data) {
    drawPoints(data[i], cluster_colors[i]);
  }
}

// 点の描画
function drawPoints(array, color) {
  let r = 6;
  noStroke();
  fill(color);
  for (let point of array) {
    ellipse(int(point[0]), int(point[1]), r, r);
  }
}