雪の結晶をシミュレーションするにはどうしたらよいか、探していたところ拡散律速凝集(DLA)にたどり着きました。 これをP5jsでブラウザ上でシミュレーションできるようにしています。
こちらを参考に作成しました。
拡散律速凝集(Diffusion-limited aggregation; DLA)
ブラウン運動する粒子が核となるクラスタに取り込まれクラスタを成長させる過程のことをいいます。 DLA によってできるクラスタはブラウン木と呼ばれる。 下図のようにフラクタルな構造になる。
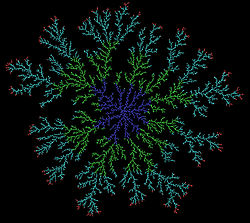
wikiより引用。
今回はこれを目指してコードを書いた。
用語説明
- ブラウン運動:浮遊する微粒子が不規則に運動する現象。シミュレーションでの青い粒の動き。
- クラスタ:同種の原子あるいは分子が相互作用によって数個以上の数が結合した物体を指す。シミュレーションでの白い粒の塊。
DLAシミュレーションのステップ
DLAによるクラスタのシミュレーションは以下のようになります。
- 中央にクラスタの核を置く。
- その周りを粒子がブラウン運動している。
- クラスタにブラウン粒子が隣接すると、粒子は結晶化する。
これを繰り返してクラスタが大きくなります。
いくつかのパターン
今回のシミュレーションで出来たブラウン木の一部。 結晶の粒子数が40,000を超えたあたりの様子が以下になっています。


毎回異なるパターンになるので一期一会を楽しんでください。
シミュレーション
実際にDLAをシミュレーションしているのが下の図です。
- 青い丸:ブラウン運動する粒子
- 白い丸:結晶化したクラスタ
計算量の都合上、クラスタの粒子数が50,000を超えたら停止するようにしています。
ソースコードと解説
let flowing_perticles = [];
let fixed_perticles = [];
let initial_size = 300;
let porse = false;
let adsorption_distance = 6; // 吸着距離
let max_size = 50000;
frame_rate = 30;
let canvas_size = {width: 400, height: 400} //px
let center = {
x: canvas_size.width / 2,
y: canvas_size.height / 2,
}
let bg_color = null;
let flowing_color = null;
let fixed_color = null;
// 再描画
function restart() {
ini();
}
// 初期化
function ini() {
let array = [];
fixed_perticles = [new Perticle(canvas_size.width / 2, canvas_size.height / 2)];
flowing_perticles = setRandomPositions();
porse = false;
}
// 粒子をランダムに配置する
function setRandomPositions(){
let array = [];
let half = Math.floor(canvas_size.height / 2);
for(let i = 0; i < initial_size; i++){
let r = random(30, half);
let theta = random(0, 2*PI);
let x = int(center.x + r*cos(theta));
let y = int(center.y + r*sin(theta));
array.push(new Perticle(x, y));
}
return array;
}
// p5js
function setup() {
let canvas = createCanvas(canvas_size.width, canvas_size.height);
canvas.parent('canvas');
// フーレームレートを1/1secにする
frameRate(frame_rate);
bg_color = color(10, 10, 10);
flowing_color = color(0, 163, 245);
fixed_color = color(159, 217, 246);
background(bg_color);
// 描画を繰り返さない。
ini();
}
function draw() {
if (!porse) {
// 粒子の動き
action();
// 描画
background(bg_color);
drawPerticles(flowing_perticles, flowing_color);
drawPerticles(fixed_perticles, fixed_color);
document.getElementById('count').innerHTML = fixed_perticles.length;
if (fixed_perticles.length > max_size){
// 一定のクラスタ数で止める
porse = true;
}
}else{
// 停止中はクラスタだけ表示
background(bg_color);
drawPerticles(fixed_perticles, fixed_color);
}
}
// 粒子の動き
function action(){
// 粒子が動く
for (let flow of flowing_perticles) {
flow.move();
}
let to_fix = [];
let remove = [];
// 新しく結晶化した300個だけ比較する
let not_compare = Math.max(0, fixed_perticles.length - 10000);
for(let i in flowing_perticles){
let flow = flowing_perticles[i];
// 描画範囲外の判定
if(is_out(flow)){
remove.push(i);
continue;
}
// 吸着の判定
for (let j = fixed_perticles.length - 1; not_compare <= j; j--){
let fixed = fixed_perticles[j];
// if(abs(fixed.x - flow.x) > adsorption_distance){
// // x軸が吸着距離より離れているとき
// continue;
// }
if(is_closed(flow, fixed)){
to_fix.push(flow); // クラスタに追加する粒子
remove.push(i); // 取り除く粒子
continue;
}
}
}
// 吸着した粒子を固定する
fixed_perticles = fixed_perticles.concat(to_fix);
// 粒子を除き新たに生成する
let half = Math.floor(canvas_size.height / 2);
for(let i of remove){
// randomな初期値
let r = random(half / 2, half);
let theta = random(0, 2*PI);
let x = int(center.x + r*cos(theta));
let y = int(center.y + r*sin(theta));
flowing_perticles[i] = new Perticle(x, y);
}
}
// 近接したか判定
function is_closed(a, b){
// ユークリッド距離
// let d = Math.sqrt(Math.pow(a.x - b.x, 2) + Math.pow(a.y - b.y, 2));
// マンハッタン距離
let d = abs(a.x - b.x) + abs(a.y - b.y);
if( d < adsorption_distance){
return true;
}
return false;
}
// 描画範囲外か判定
function is_out(a){
if(a.x < 0 || canvas_size.width < a.x ||
a.y < 0 || canvas_size.height < a.y){
return true;
}
return false;
}
function drawPerticles(array, color){
let r = adsorption_distance;
noStroke();
fill(color);
for(let ele of array){
ellipse(int(ele.x), int(ele.y), r, r);
}
}
class Perticle{
constructor(x, y){
this.x = x;
this.y = y;
this.r = 5;
}
// ブラウン運動
move(){
let r = random(0, this.r);
let theta = random(0, 2 * PI);
this.x += r * cos(theta);
this.y += r * sin(theta);
}
}
参考
Webサイト
書籍
IoTで気象データを扱うためには、気象のことを知る必要があると思い読んでいる本です。 今回の雪の結晶が出来る過程も詳細に載っています。 今まで工学・情報学の知識に偏っていたので、熱や流体のとらえ方が新鮮で面白いです。
【Electron】PCのスリープと起動イベントを検知する
ElectronNodejsJavaScriptTypeScriptschedule2021-09-06
axiosでリクエスト中の処理をキャンセルする
JavaScriptNodejsschedule2021-08-31
Node.jsでChrome.exeを起動してページを開く方法
NodejsJavaScriptWindowsschedule2021-08-25
【p5js】パーリンノイズとeraseを使ったブックカバー#PCD2021
p5jsProcessingPCD2021JavaScriptschedule2021-02-20
【p5js】砂丘の砂紋のアニメーション#PCD2021
p5jsProcessingPCD2021JavaScriptschedule2021-02-17
個人の技術ブログを作り直しました(3回目)
ブログNuxtjsVuejsTypeScriptJavaScriptNetlifyschedule2020-12-19
nuxt/contentでサイトマップを作る
NuxtjsVuejsTypeScriptJavaScriptschedule2020-12-16
remarkでnuxt/contentのマークダウン書式を拡張する
NuxtjsVuejsTypeScriptJavaScriptschedule2020-12-13